Darcian Flow in Fractured Porous Media
We use mixed-hybrid finite element method for solving Darcy flow problems with 3D-2D and 2D-1D coupling between meshes of different dimensions. For compatible meshes, the pressure can be different on both sides of a fracture (or on arbitrary number of 2D manifolds connected to a 1D channel). The advantage of the mixed-hybrid formulation is better approximation of the velocity field. According to theoretical results and practical tests this method provides second order convergence of the L2-error for both the pressure and the velocity field. More over the velocity field is perfectly mass conservative.
Hybridization leads to linear systems, where two successive Schur complements can be explicitly formed in efficient way, thus the resulting system is positive definite and well conditioned.
Flow123d includes one model for a saturated medium and one model for variably saturated medium (Richards equation). The first one use MH formulation, discretizing the source term and the time term as piecewise constant on elements. While this approach is simpler and natural the discrete maximum principle is violated for short time steps possibly leading to instability and oscillations. The second model instead use lumped MH method, where source and time terms are discretized on edges. This guarantees stability even for short time steps that may be necessary for the non-linear Richards equation. Simple Pickard iterations and adaptive time stepping are used.
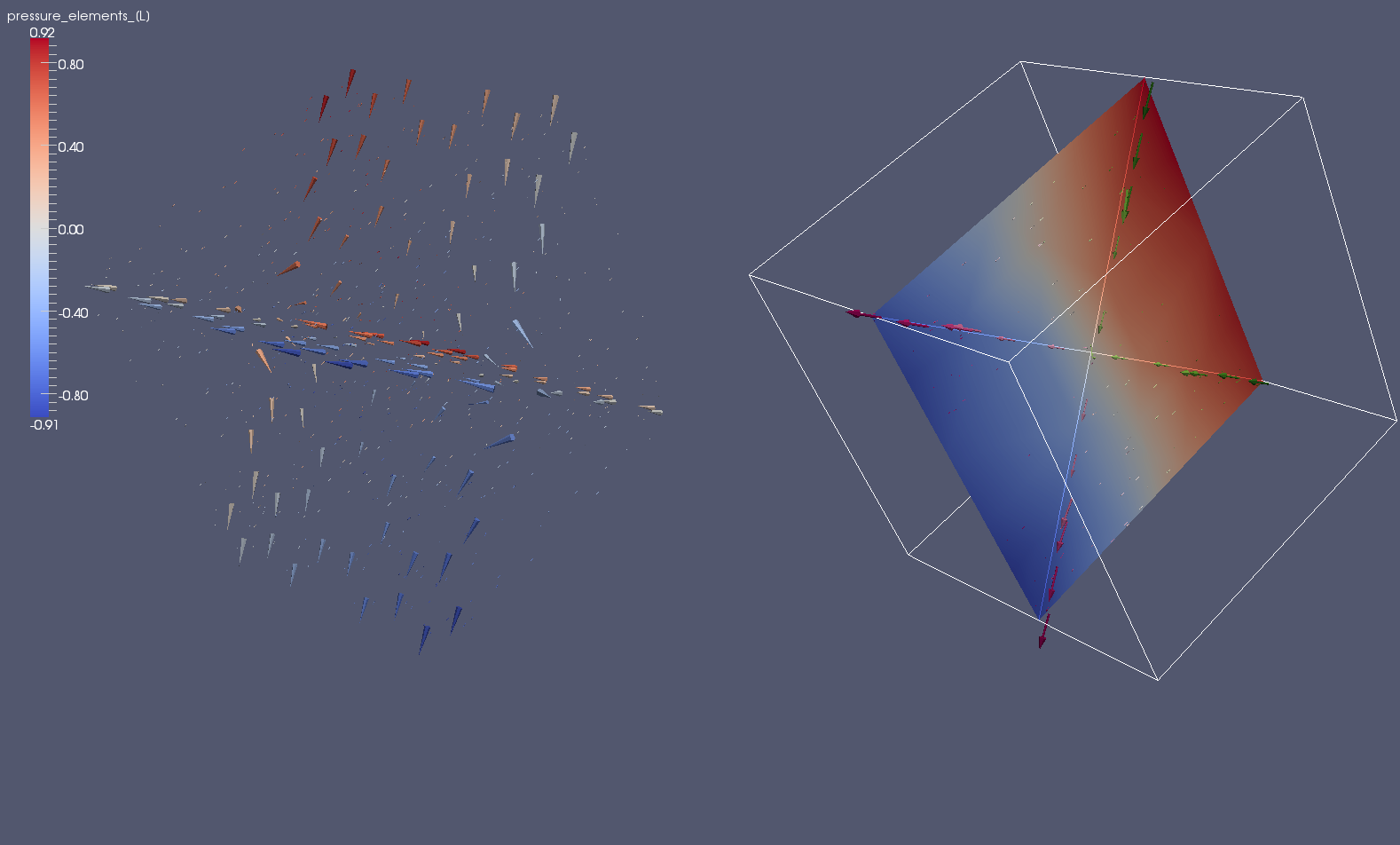
Figure: Flow field and the pressure distribution on cube with two fractures
Scalable BDDC Solver
In cooperation with Jakub Šístek, we have adopted multi-level balancing domain decomposition by constrains, namely its package BDDCML. We have demonstrated strong scaling on real Darcy flow problems up to 1000 processors, see the preprint.
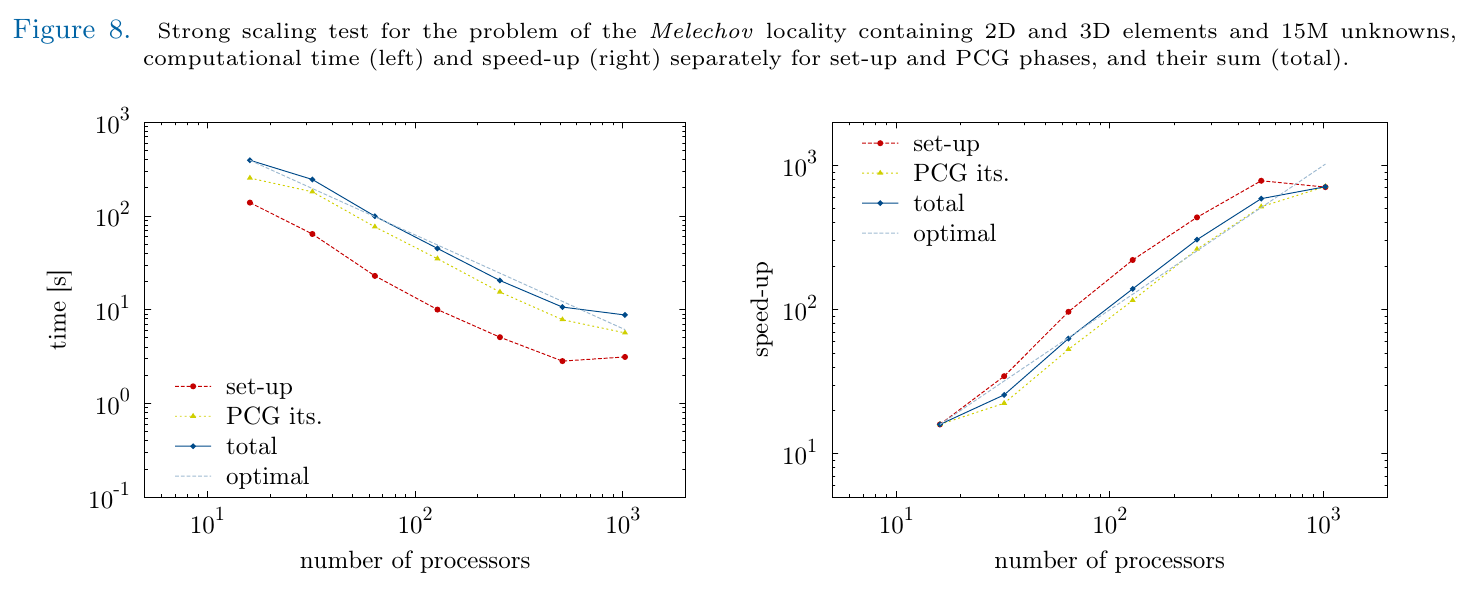
Figure

